Table of Contents

Present Value: Definition, Criticisms & Example

What is Present Value

Present value (PV) is the current value of a future sum of money, or stream of revenue. For example, Business A may be expecting to receive $3 billion in revenue in two years’ time. The PV calculates what that $3 billion would be in today’s money.

The PV is calculated using the discount rate. This is the rate used to work out what future cash flows will be worth today. It is usually based on the anticipated rate of inflation which would effectively erode the future value (FV). In other words, the present value calculates the value of income or existing funds, in today’s money.

The issue with assigning the discount rate with an inflationary rate is that inflation can be highly unpredictable. Instead, investors use a potential alternative investment. For example, a savings bond may offer 5 percent interest. This then provides a viable comparison for the project against the investment in today’s money.

Key Points

Present Value (PV) is the current value of a potential future sum of money.
The PV can be calculated using the formula: PV = Future Value / (1+r)^n (where r = interest rate, and n = number of years)

The PV is usually calculated by using a future value and applying a discount rate in order to obtain the present value. For example, Mr. Foley wants to have $110 next year, and is able to obtain a rate of return of 10 percent. Based on this, he wants to know how much to invest in order to obtain the future value of $110.

The present value is therefore the future value ($110) divided by the rate of return (10 percent), which represents 1.1. The end result is $100, which is the present value of $110 when the discount rate is equal to 10 percent.

Why Is Present Value Important?

Present value is important as it gives investors the ability to determine whether their investment will be worth it in future years. For example, $1,000 today will not be worth the same in five years’ time – presenting an inflationary risk. At the same time, there is the opportunity cost to factor in. There are alternative investments which may be safer and offer a higher rate of return.

So present value works out whether an investment would bring greater returns than an alternative. For example, we may be presented with an investment opportunity – take $1,000 today, or, wait five years and receive $1,500. Now, we could take the $1,000 and invest it in a savings account earning 5 percent interest each year. This would take us to roughly $1,285 after five years, which would suggest the other option is better.

However, investors may want to know how much they need to invest today in order to have $1,500 in five years time. This can be calculated using the formula:

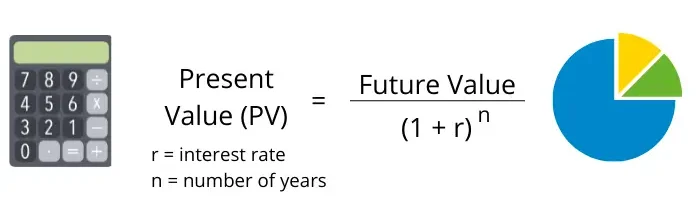
So in this case Present Value = $1,500 / (1+0.05)5 which equals 1,500/ 1.2762815625.

This would mean that in order to make $1,500 over a period of five years, we would need $1,175 today, earning a compound interest rate of 5 percent.

This concept is important because an investor with money has two options. They can either save it in a bank, or, they can invest it into a business venture, stocks, bonds, or other investment opportunity. By finding out what the present value is of a future investment opportunity, they are able to calculate whether the additional risk is worth the potential higher investment return.

How Do You Calculate Present Value?

We can calculate present value by taking the future sum of an investment and using the discount rate to provide its value at the present day. In order to calculate the present value, there are three main variables which are needed. They are the anticipated value of the investment, number of years of that investment, and the discount rate.

The importance of the discount rate is crucial to the calculation. A higher rate can lead to a low present value, whilst a low discount rate will lead to a high present value.

Once these variables have been obtained, investors can use the formula below:

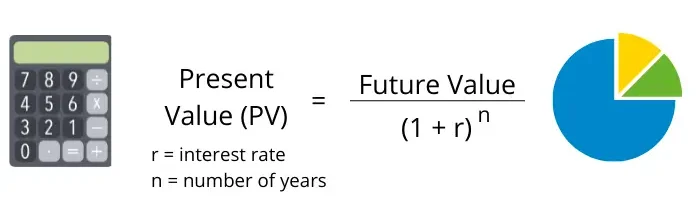
We can then calculate present value by following the steps below:

Add the future value to the numerator of the formula.
Determine the discount rate and add this to the denominator of the formula. (Note: this must be in its decimal form, e.g. 5 percent = 0.05)
Add the number of years into the denominator field marked ‘n’.
Calculate the denominator sum first by adding 1 to the discount rate. Once calculated, use the years to determine the power of this figure.
Once the denominator value is known, divide the top value (future value), by the bottom figure. Alternatively, there are many online calculators which are available, such as this present value calculator.

Criticism of Present Value

One of the requirements of calculating present value involves assuming a discount rate. This is the return which an investor could earn on those funds over a set period. However, economics is dynamic. A rate which might be reasonable today is often way off in a year or two.

One example of this issue is the resulting inflation which occurred after the 2020 Coronavirus epidemic. For an investor looking to calculate present value, they may have used a low rate which was present at the time. Yet rates increased in the years after, meaning those calculations will lead to an overestimation.

Present Value vs Future Value

What is the difference between present value and future value? Well future value (FV) is the value of an asset after a specified date in the future. This is based upon an assumed rate of return, whereby investors leave the investment returns, with the asset compounding on a set basis.

The future value therefore provides a useful barometer for different types of investments. By calculating how much an investment today would bring in over x number of years, it allows investors to compare potential investments.

By contrast, present value is calculated using the future value. This is where a future value is known, but investors want to know how much they need to invest in order to obtain that end goal. For example, the future value of an investment is anticipated to be worth $1,000 in 5 years. However, the present value looks at what that $1,000 would be in today’s money.

This is calculated using a discount rate, which is the anticipated rate of return on an investment over a set period of time. This is then ‘discounted’ from the future value, to find out how much would be needed in today’s money, to achieve a set future value.

Present Value Example

An investor has the choice between receiving $1,000 today, earning 4 percent interest per year, or, $1,500 in five years’ time. So which is the best option for the investor?

Well there are two options:

$1,000 today earning 4 percent interest over five years.
$1,500 in five years.

In the first scenario, we are missing the future value – the value it will be in five years time. This can be calculated using the future value formula:

So in the first scenario, we have the present value ($1,000), the interest rate (4%) and the number of years (5). This can then be calculated using the formula: Future Value = $1,000 (1+0.04)^5 = $1,000 x (1.2166529024) = $1,216.65

In the second scenario, we have the future value ($1,500), the number of years (5), and we can assume the same discount rate (4 percent). So using the formula, we would calculate this as: Present Value = $1,500 / (1+0.04)^5 = $1,500 / (1.2166529024) = $1,232.89

The two options could then be summarised as follows:

$1,000 today earning 4 percent interest over five years would equal $1,216 at the end.
The $1,500 is the equivalent of $1,232.89 in todays money – meaning it is higher than the alternatives present value of $1,000.

Therefore, option two would be the best choice.

FAQs

How do you calculate present value?

You can calculate present value using the formula PV = Future Value / (1+r)^n, where r = interest rate and n = number of years.

What is the present value of money?

Present value (PV) is current value of a future sum of money. In other words, it calculates what $x,xxx would be worth today if that is what you would receive in say five years time.

What is an example of present value?

Let’s say you are offered two options: receive $1,000 today, or wait five years and receive $1,500. The PV calculates how much the future sum would be in today’s money – thereby giving a clearer comparison to help choose between the options.

About Paul

Paul Boyce is an economics editor with over 10 years experience in the industry. Currently working as a consultant within the financial services sector, Paul is the CEO and chief editor of BoyceWire. He has written publications for FEE, the Mises Institute, and many others.