Table of Contents

Capital Markets: Definition, Types & Functions

Written by Paul Boyce Posted in Macroeconomics
Last Updated April 11, 2023

What are Capital Markets

Capital markets are where savers come to invest their capital in long term investments such as corporate debt, equity-backed securities, and government bonds. In other words, savers – those with capital – come to invest and those who need capital come to borrow. So businesses come to the capital markets in order to borrow money to finance a new infrastructure project they are undertaking – these are known as corporate bonds.

Capital markets deal with long term debt that allows businesses and governments to secure capital to allow them to invest and provide public services. This is defined as anything over one year. Anything under one year or less is considered within the money markets – where the money is far more liquid.

Key Points

Capital markets are where investors (those with capital) come to lend to borrowers (those who need capital).
Capital markets refer to long-term issues of debt (over one year), which contrasts to money markets that covers short-term debts.
The two main types of capital markets are primary and secondary. The primary market is where new debt and equity is issued – whilst the secondary market is where old debt and equities are traded between investors.

Simply put, capital markets deal with long term debt such as stocks and bonds – whereby the capital is used for long term investments that expand the business and increase revenues. By contrast, the money market focuses on short-term debt that focuses on funding day to day activities – examples include deposits, collateral loans, acceptances, and bills of exchange.

Capital markets are split into two categories – the primary market, and the secondary market. The primary market is where businesses and governments go to get fresh capital. In other words, investors go there to lend out money with fresh new debt being issued.

We then have the secondary market. This is essentially where old debt is traded. In other words, investors go to this market to exchange cash in return for debt that has already been issued. For instance, a hedge fund may go to the S&P 500 to buy stocks in Alphabet. The cash has already been invested in Alphabet with the hedge fund receiving stocks. In the secondary market, the equity (stocks) are sold again in return for cash.

Types of Capital Markets

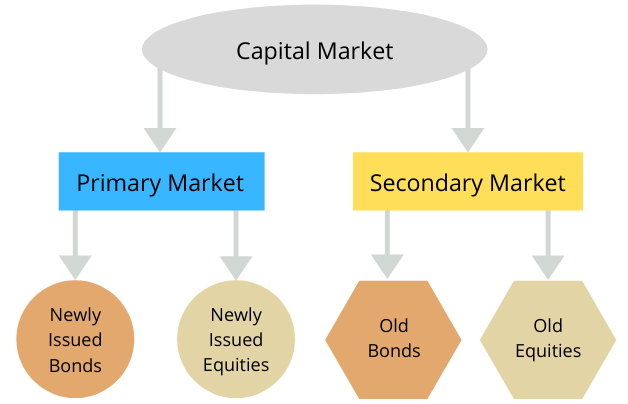
Primary Market

The primary capital market is where new debt or stocks are issued. This might come in the form of government bonds, or, alternatively, shares in a company.

Otherwise known as the ‘New Issues Market’ – it is where businesses and governments come to find new money. That new money is then transferred into either debt or shares in the company. It is locked in either: until they are sold in the secondary market; the debt expires; or, the company issues a buyback on its stocks.

There are two main types of financial instruments that are traded in the primary capital market. They are equities (stocks) and debt. Equities are commonly bought and sold via the stock market such as the New York Stock Exchange.

These new equities are introduced via an Initial Public Offering (IPO). This is simply where companies offer part of their company to the public in return for capital.

“Otherwise known as the ‘New Issues Market’, the Primary market is where new debt and equities are sold.”

By contrast, the market for bonds is slightly more convoluted. In essence, bonds are issued through an intermediary – the underwriter. So Company A goes to the underwriter to issue bonds worth $1 million. The underwriter then issues those bonds and sells them to its investors and clients.

The point of the underwriter is to ensure that Company A receives the capital it needs. So the underwriter essentially pays Company A for the bonds and then sells it onto the market – usually at a higher rate. The risk is then passed onto the underwriter, but Company A is guaranteed to get the full loan.

Secondary Markets

The secondary capital market is where old debt or stocks are traded between investors. This contrasts with the primary market as the debt has already been issued. In essence, the debt is acting as real money. The value it has is the interest that is paid on it – so it acts as a passive source of revenue. Yet it is an illiquid asset in the fact that you have to sell it to actually buy goods and services in the economy.

In turn, those who don’t need liquid capital will invest in the capital markets, whilst those who need money now will go to the secondary markets to sell their bonds and equities.

In the secondary capital markets, stocks are traded between investors through stock markets such as the London Stock Exchange, the Tokyo Stock Exchange, and the New York Stock Exchange – among many more. Those who no longer want specific stocks sell them on the exchange. These are then ‘liquidated’. In other words, the seller now has cash instead.

“The secondary capital market is where old debt or stocks are traded between investors.”

Investors use the secondary markets in order to obtain cash – perhaps to invest in another stock or for private consumption. In financial terms, it is simply to liquidate assets so other things can be bought.

We then have the secondary market for bonds. In contrast to equities, bonds tend to be held for a longer period of time – usually till expiration. However, the secondary market plays an important role for those that hold bonds but need cash quickly.

The bond market is very diverse with thousands and millions of issuers across the world. Each has a different yield, maturity, and qualities. It is for this reason that the secondary market sells bonds primarily ‘Over the Counter’ (OTC).

These are sold through a broker-dealer network. The sale of the bond is directly negotiated between the bond-holder and the broker, who will match the product up with a seller within their network.

Functions of Capital Markets

1. Capital Formation

In capital markets, there are people who have no immediate need for cash – investors – and those who need cash – debtors. The capital markets allow unused capital to be invested and employed instead of sitting by idle.

So rather than have $1 million sitting under the mattress, it allows businesses the opportunity to borrow and invest in new machinery or other capital equipment. In return, the investor receives a yield and the business benefits from more productive equipment.

2. Ease of Access and Exit

In today’s day and age, capital markets have become increasingly accessible, with investors able to trade off their mobiles. The advancement of technology has made capital markets almost universally available.

All investors have to do is create an account with a broker and they are essentially ready to invest. At the same time, we now have global markets too. So that also creates greater demand for assets too – meaning people can exit the market as easily as they joined.

3. Economic Growth

By facilitating a market place for borrowers and lenders, the capital market creates a more efficient flow of capital. Businesses that need a corporate loan can come to the capital market, apply, and get it issued by an underwriter. Alternatively, it can sell some of its company onto the stock exchange in return for capital.

This helps economic growth because it takes capital that is not being used, and it employs it somewhere else in the economy. Quite simply, it stimulates demand. If businesses that need credit get it, they are able to invest. In turn, that money goes to the business that provides the capital equipment that it invested in. That money then can circulate further and further through the economy – meaning an initial $1 million investment turns into $10 million after being exchanged 10 times.

4. Liquidity of Capital

Capital markets allow those who have capital, to invest it. In return, they have ownership of a bond or equity. However, they are unable to buy a car, food, or other assets with a bond certificate – which is why it may be necessary to liquidate these.

In capital markets, it is very easy for those who have previously invested, to sell the asset on to a third party in return for liquid capital (cash). If you want to sell an asset at the current market price, there is almost always a buyer – allowing you to turn an asset into cold hard cash.

5. Regulate Prices

One of the key functions of capital markets is to ensure the price of an asset is accurate. The price of a share can increase rapidly following good news, or tank badly in reaction to a poor annual report. By having thousands of traders, the prices fluctuate to a point whereby the value of the equity is reflected in its price at that time.

At the same time, the prices for bonds can fluctuate and respond more effectively due to supply and demand. For instance, bonds are usually seen as a safer investment – so are usually preferred by investors during a recession.

6. Return on Investment

In capital markets there are enough financial instruments to suit any type of investors, whether they want a high level of risk or a low level of risk – there is something for everyone.

At the same time, capital markets provide investors with an opportunity to enhance their yield on their capital. Savings accounts offer little interest – particularly in comparison to yields on the majority of stocks. The capital market, therefore, allows investors the opportunity to make a higher rate of return – although there is an element of risk too.

Capital Market Instruments

Bond Markets

The bond market is very diverse in its offerings, which is why most of the trades in this market are done ‘Over the Counter’ (OTC). There are many different types, but let us look at the main ones below:

1. Corporate Bonds – Investment-Grade

Corporate bonds are simply businesses borrowing money in exchange for a ‘bond’ at a set rate of interest. These usually come in short-term bonds with a maturity of five years or less; intermediate bonds, with a maturity between 5 to 12 years; and long-term bonds with a maturity of over 12 years.

More specifically, investment-grade bonds are those categorised for big businesses that are highly unlikely to default. They are riskier than government bonds, yet safer than ‘junk bonds’ – so are a half-way house between risk levels.

2. Corporate Bonds – Junk bonds

Junk bonds offer a high yield – much higher than other types. Yet they also offer the highest level of risk. This is because the companies that issue these bonds are either small or unreliable. In other words, the likelihood of receiving the initial investment back is not high.

This is a good way for small to medium business to obtain capital and grow as it allows them to access credit they may not have access to otherwise.

3. Foreign Bonds

Foreign bonds are issued in the domestic country by a foreign entity in local currency. For instance, an Indian firm may want to raise some capital in the US as it is unable to raise it in the Indian capital markets. In turn, it may issue $1 million in foreign bonds – all in US dollars. The debt is therefore repayable in US dollars.

Although this can pose a greater risk to the foreign entity due to currency fluctuations, it provides an avenue to capital that may be unavailable in its own market. At the same time, it allows investors to diversify their portfolio to reduce their exposure to economic fluctuations.

4. Municipal Bonds

A municipal bond differs from a government bond in the fact that they are issued by local government or one of its agencies – rather than the central/federal government. These are generally safe bonds but present a greater risk than treasury bonds.

They can be popular as they come in a tax-exempt version, with the investment funding local infrastructural projects such as new parks, libraries, or bridges.

5. Treasury Bonds

Government bonds, or ‘treasury bonds’, as they are commonly referred to in the US, are issued by central government over a set period of time – usually greater than 10 years. They earn a small amount of interest – below the market average, due to the low risk associated with such.

These are considered the holy grail of bonds in the fact they are virtually risk-free. However, some nations have a better reputation than others. Greece, Italy, and Spain for instance present a greater risk and therefore offer a higher yield. By contrast, the US offers lower yields that represent its reliability to make repayments.

6. Zero-coupon Bonds

Zero-coupon bonds are bonds that are sold on the market at a steep discount. This is because there is no interest due until it expires – so essentially its value gains over time.

Often, these bonds are indexed to inflation to ensure the owner of the bond maintains its purchasing power throughout time.

Stock Markets

The stock market contrasts with the bond market in the fact that it’s offering is comparatively simple, with fewer choices. In fact, there are only two main types of stocks. Let us look at them below:

1. Common Stock

Common stock is generally issued on the local stock market such as the New York Stock Exchange. The primary market for this is usually created through the Initial Public Offering (IPO). This is simply where the company sells a percentage of their company in return for capital.

When we are talking about common stocks, these are the most referenced type of stocks there are. In fact, when referring to stocks, these are the default type that we refer to. This is because they are issued in a greater quantity by firms – which almost means there is a greater number of them available on the market.

The common stock grants the owner a stake in the company, thereby allowing the owner a say in major management decisions. At the same time, owners of common stocks are also entitled to dividend payments where and when issued.

In general, these are seen as riskier investments than bonds due to the volatility but offer higher yields over the long term. This comes with the associated risk of the company going bankrupt – common stockholders are at the back of the queue when it comes to default payments. They are behind creditors, bondholders, and preferred stockholders. So, in the event of a default, they are very unlikely to see much of their initial investment back.

2. Preferred Stock

Preferred stocks are more specific to each company. They offer a fixed dividend that is due each year but is not guaranteed if the company has financial difficulties. However, the dividend can be backdated, meaning it is liable to be paid in the future.

Preferred stockholders also benefit from a higher dividend rate than common stockholders. At the same time, their dividend is also the last to be cut – meaning a company that’s experiencing financial difficulty will cut common stock dividends first.

Preferred stocks act in the same way as common stocks – you can buy them through a broker. They also represent ownership of the company. However, whilst common stocks have voting rights, preferred stocks do not. Stocks are just one of the options on the list of accredited investor opportunities.

So preferred stocks are very similar to common stocks but are similar to bonds in the fact that the owner receives a fixed rate of income over a period of time. Yet they also have similarities with common stock in the fact that they represent part of the company.

Capital Markets FAQs

What is a capital market?

What is an example of a capital market?

Capital markets refer to both the bond and equity markets. Bonds are generally sold ‘Over the Counter’ so are arranged via a brokerage such as IG or Hargreaves Lansdown. Equity markets generally deal with stocks. So these are sold through the likes of the New York Stock Exchange, the London Stock Exchange, and the Tokyo Stock Exchange.

How do capital markets work?

Capital markets work by linking the buyer or debt or securities, with investors who are willing to risk and divert their capital into various uses. It works generally through brokerage firms that offer to facilitate the transfers for a small fee.

About Paul

Paul Boyce is an economics editor with over 10 years experience in the industry. Currently working as a consultant within the financial services sector, Paul is the CEO and chief editor of BoyceWire. He has written publications for FEE, the Mises Institute, and many others.