Perpetuity: Definition, Formula, Types & Examples

What is a Perpetuity

In finance, perpetuity refers to the ongoing payment of a bond or security with no end date. It originates from the Latin phrase ‘perpetuitās’, which translates to ‘continuity’. This reflects the continuing payments to the recipient by the provider.

Pronounced as ‘per-pet-yew-ity’, it is very similar to an annuity as both guarantee a periodic payment. However, a perpetuity is a stream of cash flow that continues in forever. So although an annuity has a set expiry, a perpetuity does not.

Although a perpetuity is paid forever, it is seen as having a finite value. Now this might sound counter-intuitive, but let’s think about it. A continual series of cash flows will lose its value over time. For example $100 will not be worth the same in ten years time. Even less so in one hundred years.

If the cash flow is $100 today, in 200 years time, it is likely to be worth less than pennies in todays present value. In fact, it will become so worthless than any subsequent years cash flow will become meaningless to the final figure of the perpetuity.

As perpetuity has a finite value over the long-term, businesses and investors can use it to calculate the value of assets or help with capital budgeting. This might be assets such as real estate, bonds, stocks, or annuities. For example, a preferred shareholder receives fixed dividend payments. By using the perpetuity formula, we can find out the present value of the preferred dividends.

Perpetuity Formula

To find out the value of a perpetuity, there are two formula’s. The first of which is a simple version of valuation, as seen below:

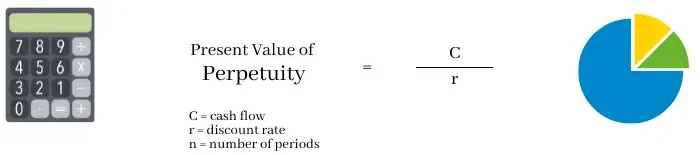
The simple way to calculate perpetuity is to take the cash flow and divide by the discount rate. For the purpose of this calculation, the discount rate is an artificial figure which may represent the banks interest rate, inflation, or the interest rate of alternative investments.

Using this formula, we can take an example. An investor may earn $1,000 in annual dividends from their preferred stock in perpetuity. This represents their cash flow. We then take a discount rate of 5 percent, which as a figure, is 0.05. So the calculation would be $1,000 / 0.05, which equals $20,000.

We may want to find out how much the perpetuity would be worth over the course of a number of years. So we can calculate that using the formula:

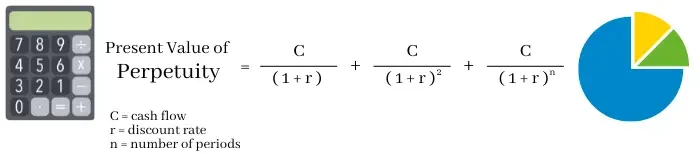
In this formula, we take the cash flow and divide by one plus the discount rate. For subsequent years, we add one with the discount rate and multiple this to the power of the number of years. For instance, a cash flow of $1,000 and discount rate of 5 percent would equal $952.38 in year 1, $907.03 in year 2, and $863.84 in year 3. This would equal a present value of $2,723.25 over a 3 year period. However, in the long-run, this calculation has virtually the same result as the simple perpetuity formula.

Examples of Perpetuity

Real estate

Real estate is a typical example of perpetuity. For those who purchase an apartment and rent it out, that rental income is a continual payment. The rent that landlords receive is defined as a perpetuity. It is paid out in yearly instalments and has no end date. Whilst tenants will come and go, there will still be a stream of income.

Consols

In 1751, the British government introduced what was known as ‘consols’. Short for ‘consolidated annuities’, these are perpetual bonds that the British issued primarily to fund war efforts. Whilst it paid out an annual stream of income over an indefinite period, these perpetuities were redeemable at the request of the British government. It was not until 2015 that the government fully redeemed and therefore discontinued its issue.

Common Stocks

When firms issue common stocks, investors pay an upfront fee in return for a share of the company and a claim to its profits through dividends. Although these payments may vary, they are paid in perpetuity. The only end date is that by which the company goes under.

Preferred Stocks

When a firm issues preferred stocks, these generally have a maturity date of up to 30 years. However, these can have an infinite lifespan, thereby providing an ongoing payment in perpetuity. The only downside is that the issuing business will have an option to redeem at any point.

Types of Perpetuity

There are two main types of perpetuities: fixed and variable. This might otherwise be known as a flat/constant perpetuity and a growing/growth perpetuity.

Flat or Constant

A flat or constant perpetuity pays an annual rate that remains the same. This means that during its life, the value of the repayments will erode away due to inflation. So a $100 payment this year will lose most of its value in one hundred years time. This is what makes these types of perpetuity viable. The cash flow gradually loses value, which is where the formula helps to calculate how much the perpetuity is worth over its useful life.

Formula

As touched on previously in this post, we can see the formula is equal to cash flows divided by the discount rate. This is the most basic formula, but provides an easy and straight forward valuation.

Growing Perpetuity

A growing perpetuity is where the cash flow grows at a specific rate each year. This is very beneficial to investors as it guarantees the purchasing power of their income.

Examples include common stocks whereby dividend payments tend to increase in line with inflation, whilst rental apartments also tend to increase prices to account for inflation.

This type of perpetuity is commonly used to determine the value of stock prices and real estate values. As these both increase in value over time, a growing valuation is required. Unfortunately, this requires a more complex formula than that of its flat/constant counterpart.

Formula

Growing perpetuity payments increase during the course of its life – which is indefinite. This increases the value of the cash flow on a yearly basis, thereby compounding the interest.

To calculate the value of a growing perpetuity, we can use the formula below:

For example, a company may receive a yearly cash flow of $5,000. That represents C in the formula. The expected rate of return is 10 percent, whilst the growth rate is 5 percent. Putting this into the formula equals $5,000 / (0.1 – 0.05) = $100,000.

Perpetuity vs Annuity

An annuity is a type of insurance or investment which pays out a fixed or variable sum over a set period of time. By contrast, a perpetuity is a type of annuity but instead of lasting for a set period of time, payments go on indefinitely.

For example, a pension is a type of annuity. Upon retirement, pensioners will use their retirement savings to purchase an annuity. The pensioner then receives an annual payment until their death. By contrast, a perpetuity is paid forever. So even in the event of death, the next of kin would inherit it and therefore continue to receive those payments.